Opérateurs différentiels

  1. Champ scalaire, champ vectoriel.

    2. Définition : un champ scalaire est la donnée en tout point M de l’espace, d’une grandeur scalaire f (M,t).

    Exemple : le potentiel électrique V ( M, t ), la température T ( M, t ).

    Un champ scalaire est donc une fonction réelle de 4 variables ( 3 variables d’espace et le temps ).

    En coordonnées cartésiennes : f ( x, y, z, t ) ; cylindriques : f ( r, q , z, t ) ; sphériques : f ( r, q , j ).

    Définition : un champ vectoriel est la donnée en tout point M de l’espace, d’un vecteur a (M,t).

    Exemple : le champ électrique E ( M, t ), la vitesse v ( M, t ).

    Un champ vectoriel est donc une fonction de 4 variables ( 3 variables d’espace et le temps ) dans R3.

    En coordonnées cartésiennes : E ( x, y, z, t ) = Ex ( x, y, z, t ) ex + Ey ( x, y, z, t ) ey + Ez ( x, y, z, t ) ez

    Ex , Ey, Ez sont trois champs scalaires.

    En coordonnées cylindriques : E ( r, q , z, t ) = Er ( r, q , z, t ) er + Eq ( r, q , z, t ) eq + Ez ( r, q , z, t ) ez

    En coordonnées sphériques : E ( r, q , j , t ) = Er ( r, q , j , t ) er + Eq ( r, q , j , t ) eq + Ej ( r, q , j , t ) ej

  2. Définition des opérateurs différentiels.

Les opérateurs différentiels sont des combinaisons de dérivées partielles par rapport aux coordonnées d’espace.

  1. Gradient.

    2. Le gradient s’applique à un champ scalaire f ( M, t ) et renvoie un vecteur.

    Définition : Soit f ( M,t ) un champ scalaire. Soit dl = dOM un déplacement élémentaire du point M considéré. Au cours de ce déplacement f varie de df . Le gradient du champ scalaire f ( M, t ) est le champ vectoriel grad f tel que :

    df = grad f . dl

    Expression en cartésiennes : df = et dl = dx ex + dy ey + dz ez donc

    grad f = ex + ey + ez

    Expression en cylindriques :

     

     

     

     

    Expression en sphériques :

     

     

     

     

    Propriété : en tout point M, grad f est un vecteur orthogonal à la surface équi-f qui passe par M.

    Preuve :

     

    Propriété : en tout point M, grad f est dirigé vers les f croissants

    Preuve :

  2. Divergence.

    3. La divergence s’applique à un champ vectoriel a ( M, t ) et renvoie un champ scalaire.

    Définition : soit un point M et un petit volume dV autour de M. Soit dS la surface qui délimite dV. Soit dF le flux du champ vectoriel a à travers dS. On appelle divergence en M du champ vectoriel a le scalaire div a tel que :

    dF = div ( a ) dV

     

    Expression en cartésiennes : : a ( x, y, z, t ) = ax ( x, y, z, t ) ex + ay ( x, y, z, t ) ey + az ( x, y, z, t ) ez

     

     

     

     

     

     

     

    div a = + +

    Il existe des expressions de la divergence en coordonnées cylindriques et en coordonnées sphériques mais elles sont compliquées, et pas de la même forme qu’en coordonnées cartésiennes !

    Théorème de Green – Ostrogradsky :

    Soit un volume V de l’espace et un champ vectoriel a ( M,t ). Soit S la surface qui délimite le volume V.

    Le flux de a à travers S est égal à l’intégrale de volume de div ( a ) sur le volume V.

     

     

     

     

     

     

     

     

  3. Rotationnel.

    4. Le rotationnel s’applique à un champ vectoriel et renvoie un champ vectoriel.

    Définition : soit un point N et un petit contour fermé dG autour de N.Le contour fermé délimite une petite surface dS = dS n. Soit un champ vectoriel a ( M, t ). Soit dC la circulation de a sur dG .

    Le rotationnel en N du champ vectoriel a se note rot ( a ) ( N ) et c’est le vecteur tel que :

    dC = rot ( a ) . dS

    Expression en cartésiennes :

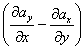    rot ( a ) = ex + ey+ ez

    Comme pour la divergence, il existe une expression du rotationnel en cylindriques et en sphériques mais elles sont compliquées et pas de la même forme qu’en cartésiennes.

    Théorème de Stokes - Ampère :

    Soit une surface ouverte S qui s’appuie sur un contour fermé G . Soit un champ vectoriel a ( M,t ).

    La circulation de a sur le contour G est égale au flux de rot ( a ) à travers S.

     

     

     

     

     

     

     

  4. Laplacien scalaire.

    5. Le Laplacien scalaire agit sur un champ scalaire et renvoie un champ scalaire.

    Expression en cartésiennes : D f =

    Expression en cylindriques ou en sphériques :compliquées et pas de la même forme !

  5. Laplacien vectoriel.

    6. Le Laplacien vectoriel agit sur un champ vectoriel et renvoie un champ vectoriel.

    Expression en cartésiennes : D a = D ax ex + D ay ey + D az ez

    Expression en cylindriques ou en sphériques :compliquées et pas de la même forme !

  6. Expression des opérateurs à l’aide du vecteur Nabla.

Le vecteur Nabla Ñ est un vecteur symbolique qui permet de noter commodément les différents opérateurs différentiels.

En coordonnées cartésiennes :

Ñ = ex + ey + ez

 

Quel que soit le système de coordonnées :

grad f = Ñ f ; div a = Ñ  . a ; rot a = Ñ ^ a ; D f = Ñ 2 f

  1. Propriétés des opérateurs.
  1. Linéarité.

    2. Tous les opérateurs différentiels sont linéaires :

    Op ( a a ) = a Op ( a ) ; Op ( a1 + a2 ) = Op ( a1 ) + Op ( a2 )

    Op ( a f ) = a Op ( f ) ; Op ( f1 + f2 ) = Op ( f1 ) + Op ( f2 )

  2. Combinaisons d’opérteurs.

div ( grad f ) = D f ; div ( rot a ) = 0 ; rot ( grad f ) = 0  ;

rot ( rot a ) = grad ( div a ) - D a