Enthalpie libre et potentiel chimique

 

  1. Enthalpie libre.
    1. Définition.

      2. L’ enthalpie libre ou fonction de Gibbs est une fonction d’état, extensive, définie par :

      G = H - TS

    2. Enthalpie libre et évolution d’un système chimique
      1. Rappel : particularités de la réaction chimique

D H = Q.

et si D H > 0 on dit que la réaction est endothermique

si D H < 0 on dit que la réaction est exothermique

D S =

Une réaction chimique est une évolution thermodynamique irréversible ( même s’il existe une réaction inverse ! ). Donc Scréée > 0. Or d’après le second principe et étant donné que l’évolution est monotherme :

D S = + Scréée

donc Q < Qrév.

      1. Condition d’évolution et d’équilibre d’un système chimique.

L’évolution est monobare donc :

Wp = - pext ( VF – VI )

Or il y a équilibre mécanique avant et après réaction donc :

Wp = - pFVF + pIVI

D’autre part la transformation est monotherme irréversible donc :

Q < Qrév = T ( SF – SI).

On applique le premier principe :

UF – UI < -pFVF + pI VI + T ( SF – SI ) + Wu

Donc :

D G < Wu.

Ceci explique l’importance particulière de la fonction enthalpie libre en thermochimie. Cette notion d’évolution du système vers un minimum de G est à l’origine de la notion de potentiel chimique étudiée au II.

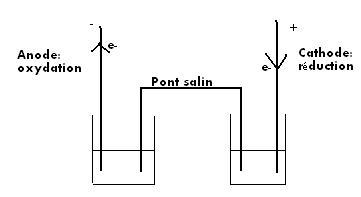
      1. Application à la pile électrochimique

Quand la pile débite, le travail élémentaire reçu par la pile est :

d Wu = - UCA. dq

or la charge débitée pour un avancement dx de la réaction d’oxydo-réduction est

dq = n. dx . F

où F est le Faraday, c’est-à-dire la valeur absolue de la charge d’une mole d’électrons :

F = NA . e

Finalement :

d Wu = - n F UCAdx .

Si l’on considère que la pile fonctionne de manière réversible,

dG = d Wu

et si de plus elle fonctionne à T et p constantes :

dG = D rG. dx

d’où l’expression de D rG :

D rG = - n F UCA.

 

    1. Relations aux dérivées partielles.
      1. Variations de G avec p et T

dG = Vdp – SdT +

On peut donc en déduire :

 

 

      1. Relation de Gibbs – Helmholtz

G = H – TS = H + T

donc H = G – T

et

soit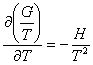

 

    1. Enthalpie libre de réaction.
      1. Définition et propriété fondamentale.

L’enthalpie libre de réaction est définie comme les autres grandeurs de réaction.

D rG = à T et p constantes.

dG = Vdp – SdT + D rG dx

D rG = D rH – T D rS

 

      1. Relations aux dérivées partielles.

        2. Les relations aux dérivées partielles pour les grandeurs de réaction D rG, D rH et D rS découlent immédiatement des relations aux dérivées partielles pour les fonctions d’état G, H et S.

        1. Variations avec T.

          2. On a :

          Preuve :

        2. Relation de Gibbs – Helmholtz.

        De même, en inversant dérivée par rapport à T et dérivée par rapport à x , on obtient la relation de Gibbs – Helmholtz pour les grandeurs de réaction :

      2. Loi de Hess.

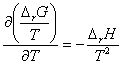
La loi de Hess étant valable pour les enthalpie et les entropies de réaction, elle est valable pour les enthalpie libres de réaction : si ( 1 ) et ( 2 ) sont deux réactions chimiques et que la réaction chimique ( 3 ) s’écrit

( 3 ) = ( 1 ) + ( 2 )

alors D rG3 = D rG1 + D rG2

  1. Potentiel chimique.
    1. Grandeur molaire partielle.
      1. Volume molaire partiel.

        2. Soit Vm1* le volume molaire du constituant 1 quand il est pur et Vm2* le volume molaire du constituant 2 quand il est pur. Quand on mélange n1 mol du constituant 1 et n2 mol du constituant 2, on obtient un mélange de volume V différent de n1Vm1* + n2Vm2* ! Ceci s’explique du fait de l’interaction des deux constituants du mélange.

        Définition : le volume molaire partiel du constituant 1 dans le mélange à T, p est

        Vm1 = à T, p et n2 constants.

        Autrement dit, si l’on a un mélange qui, à T et p, contient n1 mol de 1 et n2 mol de 2 et qu’on rajoute dn1 mol de 1, le volume du mélange va s’accroître de dV = Vm1dn1.

        Propriété fondamentale : le volume du mélange est

        V = n1 Vm1 + n2 Vm2

         

      2. Généralisation à U,H, S.

        3. Pour toute grandeur extensive, on peut définir une grandeur molaire partielle pour un constituant d’un mélange.

        Energie interne molaire partielle du constituant i :

        Umi = à T,p et nj constants

        et U =

        De même pour l’enthalpie molaire partielle Hmi et l’entropie molaire partielle Smi.

      3. Cas d’un mélange idéal.

        4. Définition : un mélange est dit idéal si ses constituants n’interagissent pas.

        On note Umi*, Hmi*, Smi*, Vmi* les grandeurs molaires du constituant i quand il est pur.

        Si le mélange est idéal, alors

        Umi = Umi*, Hmi = Hmi* et Vmi = Vmi*

        MAIS Smi¹ Smi*

        car tout mélange créée de l’entropie.

      4. Expression d’une grandeur de réaction en fonction des grandeurs molaires partielles.

      On peut exprimer facilement une grandeur de réaction en fonction des grandeurs molaires partielles des réactifs et des produits ( on note n i le coefficient stoechiométrique algébrique du constituant i ) :

      D rU = ; D rH = ; D rS=

      preuve : D rX =

    2. Potentiel chimique.
      1. Définition et propriétés fondamentales.

        2. Le potentiel chimique du constituant i est l’enthalpie libre molaire partielle du constituant i :

        µi = Gmi = à T, p et nj constants

        L’enthalpie libre du système s’écrit donc :

        G =

        et l’enthalpie libre de réaction d’une réaction chimique de coefficients stoechiométriques algébriques n i  s’écrit :

        D rG =

        Comme G diminue au cours de la réaction chimique, on voit que " ni va augmenter pour les constituants de potentiel chimique le plus bas ".

        En reprenant l’expression de dG et en écrivant que n idx = dni :

        dG = Vdp – S dT +

        Par exemple, pour le changement d’état d’un corps pur à p et T constantes, et si l’on appelle 1 et 2 les deux phases :

        dG = µ1dn1 + µ2dn2

        or par conservation de la matière :

        dn1= - dn2

        donc

        dG = ( µ2 - µ1 ) dn2

        L’évolution du système est telle que dG < 0 donc si µ2 > µ1 alors dn2 < 0 .

        L’évolution naturelle d’un système diphasé hors équilibre est de la phase de plus haut potentiel chimique vers la phase de plus bas potentiel chimique.

      2. Relations aux dérivées partielles.

        3. Les relations aux dérivées partielles pour les grandeurs molaires partielles µi, Hmi et Smi découlent immédiatement des relations aux dérivées partielles pour les fonctions d’état G, H et S.

        Conséquence pour le corps pur : dµ = Vm* dp – Sm*dT.

        et la relation de Gibbs – Helmholtz :

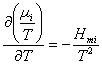
        preuve : 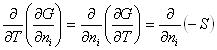et idem pour les autres…

      3. Expressions du potentiel chimique.
        1. Etat standard d’un constituant.

Définition : la pression standard est p° = 1 bar.

Définition : dans une solution, la concentration standard est C° = 1 mol.L-1.

L’état standard d’un constituant n’existe pas, c’est un état de référence qui sert à écrire le potentiel chimique du constituant i :

µi(T, p ) = µi°(T) + RT ln ( ai ) avec

        1. Mélange idéal de Gaz Parfaits.

          2. Si l’on note pi la pression partielle du constituant i dans le mélange :

          µi(T, p ) = µi°(T) + RT ln ( )

          Cas particulier : gaz parfait pur : µ ( T, p ) = µ° ( T ) + RT ln

        2. Mélange idéal de solides ou de liquides.

          3. Si l’on note xi la fraction molaire du constituant i dans le mélange :

          µi(T, p ) = µi°(T) + RT ln (xi)

          Cas particulier :solide ou liquide pur : µ(T,p) = µ°(T)

        3. Soluté dilué dans une solution idéale.

          4. Si l’on note Ci la concentration du constituant i :

          µi(T, p ) = µi°(T) + RT ln ( )

        4. Solvant dans une solution idéale.

Si l’on note xS la fraction molaire du solvant dans la solution idéale ( xS » 1 ).

µS(T, p ) = µS°(T) + RT ln (xS)

Conclusion :